with Drew Creal, Siem Jan Koopman, and André Lucas

We introduce Generalized Autoregressive Method of Moments (GaMM) dynamics. GaMM extends Generalized Method of Moments (GMM) to a setting where a subset of the parameters are expected to vary over time with unknown dynamics. To filter out the dynamic path of the time-varying parameter, we approximate the dynamics by an autoregressive process driven by the score of the local GMM criterion function. Our approach is completely observation driven, such that estimation and inference are entirely straightforward. Moreover, the approach provides a unified framework for modeling parameter instability in a context where the model and its parameters are only specified through (conditional) moment conditions, thus generalizing previous approaches built on fully specified parametric models. We provide three examples of increasing complexity to highlight the advantages of GaMM.

with Arjen Siegmann and Denitsa Stefanova

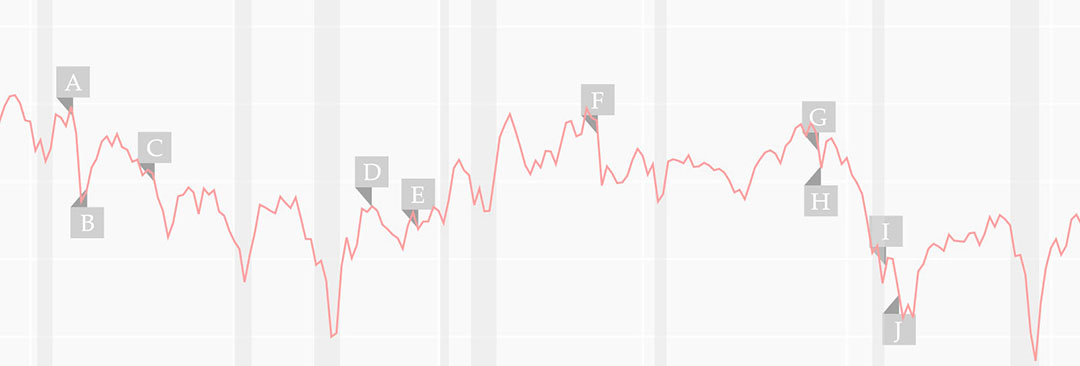
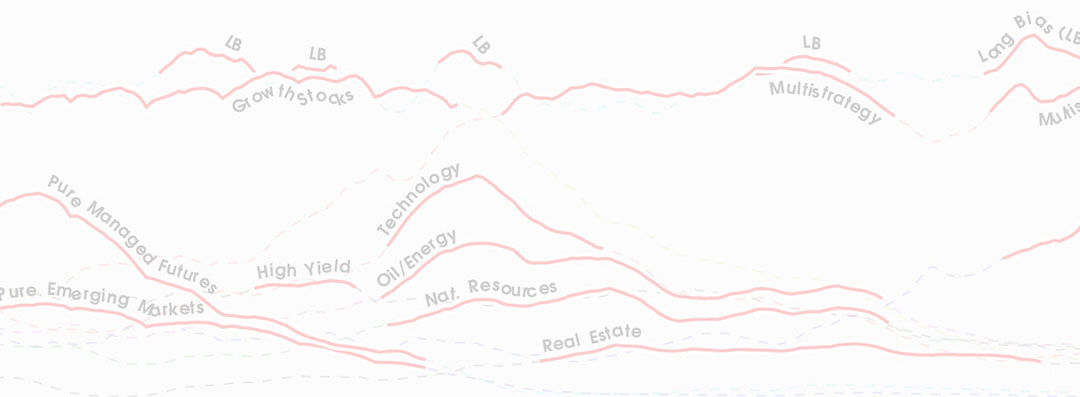
We study first-mover advantages in the hedge fund industry by clustering hedge funds based on the type of assets and instruments they trade in, sector and investment focus, and fund details. We find that early entry in a cluster is associated with higher excess returns, longer survival, higher incentive fees and lower management fees compared to funds that arrive later. Moreover, the latest entrants have a high loading on the returns of the innovators, but with lower incentive fees, and higher management fees. Cross-sectional regressions show that the outperformance of innovating funds are declining with age. The results are robust to different parameters of clustering and backfill-bias, and are not driven by the possible existence of flagship and follow-on funds. Our results show that the reported characteristics of hedge funds can be used to infer strategy-related information and suggest that specific first-mover advantages exist in the hedge fund industry.

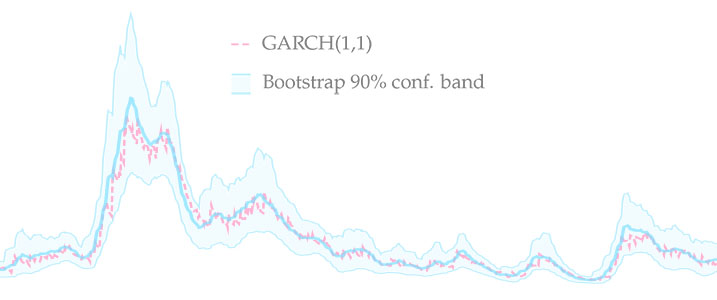
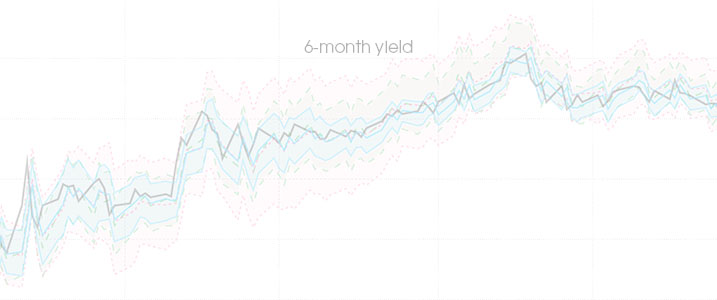
This paper is the first to propose a robust method of computing in-sample confidence bands for time-varying parameters estimated with misspecified observation-driven models. As an example of this class, I look at the family of GARCH models which are used to estimate time-varying variances and covariances. I propose a novel bootstrap procedure and a new moving-window resampler which together generate confidence bands around estimated volatility paths. The approach accounts for various sources of uncertainty, including parameter and filtering uncertainty. I illustrate the method by applying it to S&P 500 returns. Moreover, I investigate finite sample properties of the confidence bands and their convergence in a range of simulation experiments. I find that the average coverage is close to the nominal level in finite samples and that it converges to the nominal level as the sampling frequency is increased. The procedure can be used as a smoother to substantially reduce average root mean square error of GARCH paths. The new method is easily implementable and does not significantly increase the computational burden.

with Siem Jan Koopman and André Lucas

We consider score-driven time-varying parameters in dynamic yield curve models and investigate their in-sample and out-of-sample performance for two data sets. In a univariate setting, score-driven models were shown to offer competitive performance to parameter-driven models in terms of in-sample fit and quality of out-of-sample forecasts but at a lower computational cost. We investigate whether this performance and the related advantages extend to more general and higher-dimensional models. Based on an extensive Monte Carlo study, we show that in multivariate settings the advantages of score-driven models can even be more pronounced than in the univariate setting. We also show how the score-driven approach can be implemented in dynamic yield curve models and extend them to allow for the fat-tailed distributions of the disturbances and the time-variation of variances (heteroskedasticity) and covariances.

Financed from a research grant from the National Bank of Poland.