
Marcin Zamojski
Hi, I'm a research fellow at the University of Gothenburg's Centre for Finance.
I got my PhD in Finance from the Vrije Universiteit Amsterdam and Tinbergen Institute.
I do research, I teach, I do other stuff, and I skate.
Most of my research revolves about time-varying parameters and I am most captured by score driven methods. A frequentist at heart. I am also a strong believer in 'all models are wrong, but some are useful'. I am warming up to machine learning. If the data has a time dimension, count me in.
 Self-driving score filters
Self-driving score filters
Estimate any observation-driven, time-varying parameter model with only a few lines of code. Magic!
I introduce a class of approximate `score-driven' filters that is based on automatic differentiation. The agnostic approach requires that a researcher specify a conditional criterion function and that influence functions for the time-varying parameters exist theoretically. I show that in settings where a score model is assumed to be the data-generating process, self-driving filters produce comparable results to analytically derived optimal filters. The small performance loss comes as a trade-off for vastly increased simplicity and implementability. Performance of self-driving filters is also investigated in settings where optimal filters are hard or impossible to derive to see if the self-driving approach yields better results than previously proposed ad hoc solutions. The approach is applied to filters with time-varying volatility and time-varying copulas.
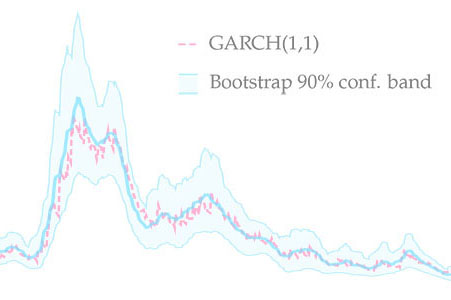 Filtering with Confidence
Filtering with Confidence
In Filtering with Confidence: In-sample Confidence Bands for GARCH Filters, I propose a novel bootstrap method which allows to obtain in-sample confidence bands for volatility paths estimated with GARCH(1,1). The new method produces bands with good coverage properties. The method is also applicable to other observation-driven models.
This paper is the first to propose a robust method of computing in-sample confidence bands for time-varying parameters estimated with misspecified observation-driven models. As an example of this class, I look at the family of GARCH models which are used to estimate time-varying variances and covariances. I propose a novel bootstrap procedure and a new moving-window resampler which together generate confidence bands around estimated volatility paths. The approach accounts for various sources of uncertainty, including parameter and filtering uncertainty. I illustrate the method by applying it to S&P 500 returns. Moreover, I investigate finite sample properties of the confidence bands and their convergence in a range of simulation experiments. I find that the average coverage is close to the nominal level in finite samples and that it converges to the nominal level as the sampling frequency is increased. The procedure can be used as a smoother to substantially reduce average root mean square error of GARCH paths. The new method is easily implementable and does not significantly increase the computational burden.
 GaMM
GaMM
Estimating time-varying parameters given a set of moment conditions. Generalized Autoregressive Method of Moments is a fast and easy to implement observation-driven method.
Generalized Autoregressive Method of Moments extends GMM to a setting where a subset of the parameters are expected to vary over time with unknown dynamics. To filter out the path of the time-varying parameter, we approximate the dynamics by an autoregressive process driven by the score of the local GMM criterion function. Our approach is completely observation driven (estimation and inference are straightforward). We provide three examples of increasing complexity to highlight the advantages of GaMM.
 Hedge Fund
Hedge Fund
Innovation
Hedge Fund Innovation discusses first-mover advantages in the secretive industry. We propose a novel method of dividing hedge funds into categories more granular than their reported style.
We study first-mover advantages in the hedge fund industry by clustering hedge funds based on a wide range of descriptors. Early entry is associated with higher excess returns, longer survival, higher incentive fees, and lower management fees. Later entrants have a high loading on the returns of the innovators. Cross-sectional regressions show that the outperformance of innovating funds are declining with age. The results are robust to different parameters of clustering and backfill-bias, and are not driven by the possible existence of flagship and follow-on funds.
 Score-driven
Score-driven
Dynamic
Nelson-Siegel
In multivariate settings the advantages of score-driven models can even be more pronounced than in the univariate setting. We are able to allow for fat-tailed distributions, conditional heteroskedasticity, and dependence in term-structure models.
We consider score-driven time-varying parameters in dynamic yield curve models and investigate their in-sample and out-of-sample performance for two data sets. In a univariate setting, score-driven models were shown to offer competitive performance to parameter-driven models in terms of in-sample fit and quality of out-of-sample forecasts but at a lower computational cost. We investigate whether this performance and the related advantages extend to more general and higher-dimensional models. Based on an extensive Monte Carlo study, we show that in multivariate settings the advantages of score-driven models can even be more pronounced than in the univariate setting. We also show how the score-driven approach can be implemented in dynamic yield curve models and extend them to allow for the fat-tailed distributions of the disturbances and the time-variation of variances (heteroskedasticity) and covariances.